SVM and Polytope Distance

Given two point sets $P=\{\bm{u}_{1},\dots,\bm{u}_{n_{1}}\}$ and $Q=\{\bm{v}_{1},\dots,\bm{v}_{n_{2}}\}$ in $\bm{R}^{d}$ , the reduced polytope distance problem (RPD) is to find two density distributions $\bm{\mu},\bm{\lambda}$ over the input points, such that $\|\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}\|$ is minimized, here $\bm{1}^{T}\bm{\mu}=\bm{1}^{T}\bm{\lambda}=1$ and $0\leq\bm{\mu},\bm{\lambda}\leq D$ for some constant $D\leq 1$ . The idea of having the upperbound $D$ is to prevent excessive influence of an outlier point. The problem can be formatted as the following optimization problem:

$\displaystyle\min_{\bm{\mu},\bm{\lambda}}\quad$	$\displaystyle\frac{1}{2}\\|\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}\\|^{2}$	(RPD)
$\displaystyle\operatorname*{s.t.}\quad$	$\displaystyle\bm{1}^{T}\bm{\mu}=1\quad\bm{1}^{T}\bm{\lambda}=1$
	$\displaystyle 0\leq\bm{\mu},\bm{\lambda}\leq D$

The RPD problem is equivalent to $C$ -SVM, but before we prove the equivalence of RPD and $C$ -SVM, we introduce an intermittent problem, the soft-margin maximization problem (S-Margin), which can be written as the following problem:

$\displaystyle\min_{\bm{w},\bm{\xi},\bm{\eta},\alpha,\beta}\quad$	$\displaystyle\frac{1}{2}\\|\bm{w}\\|^{2}-(\alpha-\beta)+D(\bm{1}^{T}\bm{\xi}+\bm% {1}^{T}\bm{\eta})$	(S-Margin)
$\displaystyle\operatorname*{s.t.}\quad$	$\displaystyle\bm{P}^{T}\bm{w}\geq\alpha\bm{1}-\bm{\xi},\quad\bm{\xi}\geq 0$
	$\displaystyle\bm{Q}^{T}\bm{w}\leq\beta\bm{1}+\bm{\eta},\quad\bm{\eta}\geq 0$

Theorem 1.

(RPD) and (S-Margin) are dual of each other.

Proof.

Consider the Lagrangian of (S-Margin):

	$\displaystyle L(\bm{w},\bm{\xi},\bm{\eta},\alpha,\beta,\bm{\mu},\bm{\lambda},% \bm{r},\bm{s})$	$\displaystyle=\frac{1}{2}\\|\bm{w}\\|^{2}-(\alpha-\beta)+D(\bm{1}^{T}\bm{\xi}+% \bm{1}^{T}\bm{\eta})$
		$\displaystyle-\bm{\mu}^{T}(\bm{P}^{T}\bm{w}-\alpha\bm{1}+\bm{\xi})-\bm{r}^{T}% \bm{\xi}$
		$\displaystyle+\bm{\lambda}^{T}(\bm{Q}^{T}\bm{w}-\beta\bm{1}-\bm{\eta})-\bm{s}^% {T}\bm{\eta}$

The KKT condition for this problem is:

	Stationary:	$\displaystyle\partial L/\partial\bm{w}=\bm{w}-\bm{P}\bm{\mu}+\bm{Q}\bm{\lambda% }=0$
		$\displaystyle\partial L/\partial\bm{\xi}=D\bm{1}-\bm{\mu}-\bm{r}=0$
		$\displaystyle\partial L/\partial\bm{\lambda}=D\bm{1}-\bm{\lambda}-\bm{s}=0$
		$\displaystyle\partial L/\partial\alpha=\bm{1}^{T}\bm{\mu}-1=0$
		$\displaystyle\partial L/\partial\beta=\bm{1}^{T}\bm{\lambda}-1=0$
	Complementary:	$\displaystyle\bm{\mu}^{T}(\bm{P}^{T}\bm{w}-\alpha\bm{1}+\bm{\xi})=0,\quad\bm{r% }^{T}\bm{\xi}=0$
		$\displaystyle\bm{\lambda}^{T}(\bm{Q}^{T}\bm{w}-\beta\bm{1}-\bm{\eta})=0,\quad% \bm{s}^{T}\bm{\eta}=0$
	Primal feasibility:	$\displaystyle\bm{P}^{T}\bm{w}\geq\alpha\bm{1}-\bm{\xi},\quad\bm{\xi}\geq 0$
		$\displaystyle\bm{Q}^{T}\bm{w}\leq\beta\bm{1}+\bm{\eta},\quad\bm{\eta}\geq 0$
	Dual feasibility:	$\displaystyle\bm{\mu},\bm{\lambda},\bm{r},\bm{s}\geq 0$

Take $\bm{w}=\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda},\bm{r}=D\bm{1}-\bm{\mu},\bm{s}=D\bm{1% }-\bm{\lambda}$ , the dual of (S-Margin) becomes:

	$\displaystyle\max_{\bm{\mu},\bm{\lambda}}\quad$	$\displaystyle L(\bm{\xi},\bm{\eta},\bm{\mu},\bm{\lambda})$
	$\displaystyle\operatorname*{s.t.}\quad$	$\displaystyle\bm{1}^{T}\bm{\mu}=\bm{1}^{T}\bm{\lambda}=1$
		$\displaystyle 0\leq\bm{\mu},\bm{\lambda}\leq D$

Furthermore,

	$\displaystyle L(\bm{\xi},\bm{\eta},\bm{\mu},\bm{\lambda})=$	$\displaystyle\frac{1}{2}\\|\bm{w}\\|^{2}-(\alpha-\beta)+D(\bm{1}^{T}\bm{\xi}+\bm% {1}^{T}\bm{\eta})$
		$\displaystyle-\bm{\mu}^{T}(\bm{P}^{T}\bm{w}-\alpha\bm{1}+\bm{\xi})-\bm{r}^{T}% \bm{\xi}$
		$\displaystyle+\bm{\lambda}^{T}(\bm{Q}^{T}\bm{w}-\beta\bm{1}-\bm{\eta})-\bm{s}^% {T}\bm{\eta}$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\\|\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}\\|^{2}-(\alpha-% \beta)+D(\bm{1}^{T}\bm{\xi}+\bm{1}^{T}\bm{\eta})$
		$\displaystyle-\bm{\mu}^{T}\bm{P}^{T}(\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda})+\alpha% \bm{1}^{T}\bm{\mu}-\bm{\xi}^{T}\bm{\mu}-(D\bm{1}-\bm{\mu})^{T}\bm{\xi}$
		$\displaystyle+\bm{\lambda}^{T}\bm{Q}^{T}(\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda})-% \beta\bm{1}^{T}\bm{\lambda}-\bm{\eta}^{T}\bm{\lambda}-(D\bm{1}-\bm{\lambda})^{% T}\bm{\eta}$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\\|\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}\\|^{2}{\color[rgb]{% 0,0,1}-(\alpha-\beta)}{\color[rgb]{1,0,0}+D\bm{1}^{T}\bm{\xi}+D\bm{1}^{T}\bm{% \eta}}$
		$\displaystyle-\bm{\mu}^{T}\bm{P}^{T}(\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}){\color% [rgb]{0,0,1}+\alpha}-\bm{\xi}^{T}\bm{\mu}{\color[rgb]{1,0,0}-D\bm{1}^{T}\bm{% \xi}}+\bm{\mu}^{T}\bm{\xi}$
		$\displaystyle+\bm{\lambda}^{T}\bm{Q}^{T}(\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}){% \color[rgb]{0,0,1}-\beta}-\bm{\eta}^{T}\bm{\lambda}{\color[rgb]{1,0,0}-D\bm{1}% ^{T}\bm{\eta}}+\bm{\lambda}^{T}\bm{\eta}$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\\|\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}\\|^{2}-(\bm{\mu}^{T% }\bm{P}^{T}-\bm{\lambda}^{T}\bm{Q}^{T})(\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda})$
	$\displaystyle=$	$\displaystyle-\frac{1}{2}\\|\bm{P}\bm{\mu}-\bm{Q}\bm{\lambda}\\|^{2},$

which is equivalent to (RPD) and completes the proof. ∎

Now we turn to the $C$ -SVM problem. The $C$ -SVM problem can be formatted as

$\displaystyle\min_{\bm{w},\bm{\xi},\bm{\eta},\gamma}\quad$	$\displaystyle\frac{1}{2}\\|\bm{w}\\|^{2}+C(\bm{1}^{T}\bm{\xi}+\bm{1}^{T}\bm{\eta})$	( $C$ -SVM)
$\displaystyle\operatorname*{s.t.}\quad$	$\displaystyle\bm{P}^{T}\bm{w}\geq(\gamma+1)\bm{1}-\bm{\xi}$
	$\displaystyle\bm{Q}^{T}\bm{w}\leq(\gamma-1)\bm{1}+\bm{\eta}$
	$\displaystyle\bm{\xi}\geq 0\quad\bm{\eta}\geq 0$

Here $C>0$ is a parameter that is chosen by the user to control the slackness. Intuitively, this problem is equivalent to (S-Margin) by fixing $(\alpha-\beta)=2$ and set $\alpha=\gamma+1,\beta=\gamma-1$ , since maximizing the soft-margin is the same as fixing the offset and minimizing the norm of the normal vector $\bm{w}$ . The formal proof is given in Theorem 2.

Theorem 2.

With an appropriate choice of the parameters $C$ and $D$ , the problems (S-Margin) and ( $C$ -SVM) are equivalent if the optimal objective is strictly greater than 0.

Proof.

Recall that $(\bar{\bm{w}},\bar{\bm{\xi}},\bar{\bm{\eta}},\bar{\alpha},\bar{\beta},\bar{\bm% {\mu}},\bar{\bm{\lambda}})$ is a KKT point of (S-Margin) if it satisfies:

Stationary:	$\displaystyle\bar{\bm{w}}-\bm{P}\bar{\bm{\mu}}+\bm{Q}\bar{\bm{\lambda}}=0$	(1)
	$\displaystyle D\bm{1}-\bar{\bm{\mu}}\geq 0$
	$\displaystyle D\bm{1}-\bar{\bm{\lambda}}\geq 0$
	$\displaystyle\bm{1}^{T}\bar{\bm{\mu}}-1=0$
	$\displaystyle\bm{1}^{T}\bar{\bm{\lambda}}-1=0$
Complementary:	$\displaystyle\bar{\bm{\mu}}^{T}(\bm{P}^{T}\bar{\bm{w}}-\alpha\bm{1}+\bar{\bm{% \xi}})=0,\quad(D\bm{1}-\bar{\bm{\mu}})^{T}\bar{\bm{\xi}}=0$
	$\displaystyle\bar{\bm{\lambda}}^{T}(\bm{Q}^{T}\bar{\bm{w}}-\beta\bm{1}-\bar{% \bm{\eta}})=0,\quad(D\bm{1}-\bar{\bm{\lambda}})^{T}\bar{\bm{\eta}}=0$
Primal feasibility:	$\displaystyle\bm{P}^{T}\bar{\bm{w}}\geq\alpha\bm{1}-\bar{\bm{\xi}},\quad\bar{% \bm{\xi}}\geq 0$
	$\displaystyle\bm{Q}^{T}\bar{\bm{w}}\leq\beta\bm{1}+\bar{\bm{\eta}},\quad\bar{% \bm{\eta}}\geq 0$
Dual feasibility:	$\displaystyle\bar{\bm{\mu}},\bar{\bm{\lambda}}\geq 0$

Each KKT point $(\hat{\bm{w}},\hat{\bm{\xi}},\hat{\bm{\eta}},\hat{\gamma},\hat{\bm{\mu}},\hat{% \bm{\lambda}})$ of ( $C$ -SVM) satisfies:

Stationary:	$\displaystyle\hat{\bm{w}}-\bm{P}\hat{\bm{\mu}}+\bm{Q}\hat{\bm{\lambda}}=0$	(2)
	$\displaystyle C\bm{1}-\hat{\bm{\mu}}\geq 0$
	$\displaystyle C\bm{1}-\hat{\bm{\lambda}}\geq 0$
	$\displaystyle\bm{1}^{T}\hat{\bm{\mu}}-\bm{1}^{T}\hat{\bm{\lambda}}=0$
Complementary:	$\displaystyle\hat{\bm{\mu}}^{T}(\bm{P}^{T}\hat{\bm{w}}-(\hat{\gamma}+1)\bm{1}+% \hat{\bm{\xi}})=0,\quad(C\bm{1}-\hat{\bm{\mu}})^{T}\hat{\bm{\xi}}=0$
	$\displaystyle\hat{\bm{\lambda}}^{T}(\bm{Q}^{T}\hat{\bm{w}}-(\hat{\gamma}-1)\bm% {1}-\hat{\bm{\eta}})=0,\quad(C\bm{1}-\hat{\bm{\lambda}})^{T}\hat{\bm{\eta}}=0$
Primal feasibility:	$\displaystyle\bm{P}^{T}\hat{\bm{w}}\leq(\hat{\gamma}+1)\bm{1}-\hat{\bm{\xi}},% \quad\hat{\bm{\xi}}\geq 0$
	$\displaystyle\bm{Q}^{T}\hat{\bm{w}}\geq(\hat{\gamma}-1)\bm{1}+\hat{\bm{\eta}},% \quad\hat{\bm{\eta}}\geq 0$
Dual feasibility:	$\displaystyle\hat{\bm{\mu}},\hat{\bm{\lambda}}\geq 0$

Assuming $\tilde{\alpha}-\tilde{\beta}>0$ , set $\delta=\frac{2}{\tilde{\alpha}-\tilde{\beta}},\tilde{\alpha}=\frac{\hat{\gamma% }+1}{\delta},\tilde{\beta}=\frac{\hat{\gamma}-1}{\delta},\tilde{\bm{w}}=\frac{% \hat{\bm{w}}}{\delta},\tilde{\bm{\xi}}=\frac{\hat{\bm{\xi}}}{\delta},\tilde{% \bm{\eta}}=\frac{\hat{\bm{\eta}}}{\delta},\tilde{\bm{\mu}}=\frac{\hat{\bm{\mu}% }}{\delta},\tilde{\bm{\lambda}}=\frac{\hat{\bm{\lambda}}}{\delta}$ , and $\bm{1}^{T}\hat{\bm{\mu}}=\bm{1}^{T}\hat{\bm{\lambda}}=\delta$ , and take $D=\frac{C}{\delta}$ , we have:

Stationary:	$\displaystyle\tilde{\bm{w}}-\bm{P}\tilde{\bm{\mu}}+\bm{Q}\tilde{\bm{\lambda}}=0$	(3)
	$\displaystyle D\bm{1}-\tilde{\bm{\mu}}\geq 0$
	$\displaystyle D\bm{1}-\tilde{\bm{\lambda}}\geq 0$
	$\displaystyle\bm{1}^{T}\tilde{\bm{\mu}}=\bm{1}^{T}\tilde{\bm{\lambda}}=1$
Complementary:	$\displaystyle\tilde{\bm{\mu}}^{T}(\bm{P}^{T}\tilde{\bm{w}}-\tilde{\alpha}\bm{1% }+\tilde{\bm{\xi}})=0,\quad(D\bm{1}-\tilde{\bm{\mu}})^{T}\tilde{\bm{\xi}}=0$
	$\displaystyle\tilde{\bm{\lambda}}^{T}(\bm{Q}^{T}\tilde{\bm{w}}-\tilde{\beta}% \bm{1}-\tilde{\bm{\eta}})=0,\quad(D\bm{1}-\tilde{\bm{\lambda}})^{T}\tilde{\bm{% \eta}}=0$
Primal feasibility:	$\displaystyle\bm{P}^{T}\tilde{\bm{w}}\leq\tilde{\alpha}\bm{1}-\tilde{\bm{\xi}}% ,\quad\tilde{\bm{\xi}}\geq 0$
	$\displaystyle\bm{Q}^{T}\tilde{\bm{w}}\geq\tilde{\beta}\bm{1}+\tilde{\bm{\eta}}% ,\quad\tilde{\bm{\eta}}\geq 0$
Dual feasibility:	$\displaystyle\tilde{\bm{\mu}},\tilde{\bm{\lambda}}\geq 0$

which coincides with (1), and implies that $(\tilde{\bm{w}},\tilde{\bm{\xi}},\tilde{\bm{\eta}},\tilde{\alpha},\tilde{\beta% },\tilde{\bm{\mu}},\tilde{\bm{\lambda}})$ is a KKT point to (S-Margin). The assumption $\tilde{\alpha}-\tilde{\beta}>0$ is from the strong duality of (S-Margin):

\frac{1}{2}\|\tilde{\bm{w}}\|^{2}+D(\bm{1}^{T}\tilde{\bm{\xi}}+\bm{1}^{T}% \tilde{\bm{\eta}})-(\tilde{\alpha}-\tilde{\beta})=-\frac{1}{2}\|\bm{P}\tilde{% \bm{\mu}}-\bm{Q}\tilde{\bm{\lambda}}\|^{2}<0,

where we assume the objective value is strictly greater than 0, i.e. the reduced convex hulls are linear separable. ∎

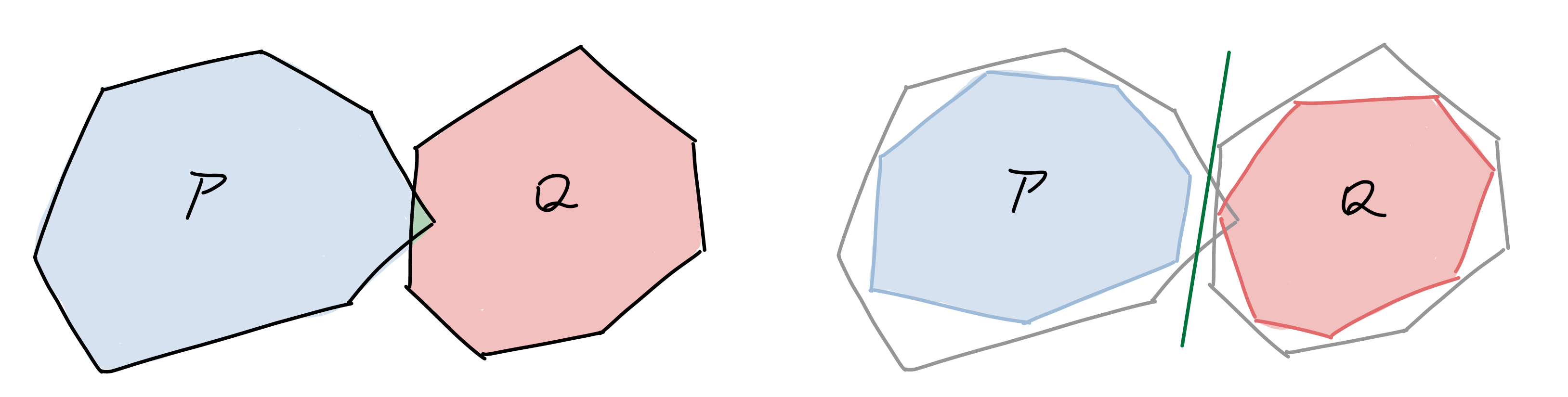
The figure below illustrates how the reduced polytope works. The left picture shows the original problem where the polytopes are not linearly separable, which corresponds to the parameter choice $D=1$ . The right picture shows an example of reduced polytope, where the reduced polytopes are linearly separable, and it corresponds to the case when the parameter $D<1$ .

References

[1] K. P. Bennett and E. J. Bredensteiner (2000) Duality and geometry in svm classifiers. In ICML, Vol. 2000, pp. 57–64.
[2] B. Gärtner and M. Jaggi (2009) Coresets for polytope distance. In Proceedings of the twenty-fifth annual symposium on Computational geometry, pp. 33–42.